In physics, energy is defined as the ability to do work or cause a change in a system. Energy can exist in many forms, such as mechanical, electrical, chemical, thermal, nuclear, and electromagnetic.
From an engineering perspective, energy is a fundamental concept that is essential for understanding the behavior and operation of physical systems. Engineers often work with energy in the context of designing, building, and operating machines, devices, and systems that utilize energy to perform various tasks.
There are different types of energy, such as potential energy, kinetic energy, and thermal energy. Potential energy is energy that is stored in a system due to its position or configuration, while kinetic energy is the energy of motion. Thermal energy is the energy associated with the temperature of a system, and it is related to the movement of the particles that make up the system.
Energy can be transformed from one form to another, and the law of conservation of energy states that the total amount of energy in a closed system remains constant over time, although it can be converted from one form to another. This principle is important for engineering applications, as engineers need to understand how to conserve and transfer energy in various systems.
Energy vs. Power
Energy is a scalar quantity that represents the capacity of a physical system to do work. It is a measure of the potential for a system to exert a force over a distance. The units of energy are joules (J) in the International System of Units (SI), although other units such as calories and electron volts are also commonly used. Energy can take many forms, including kinetic energy (the energy of motion), potential energy (the energy of position), thermal energy (the energy of heat), and electromagnetic energy (the energy of light).
Power, on the other hand, is a measure of how quickly energy is being transferred or used. It is the rate at which work is done or energy is expended over time. Power is a scalar quantity that is equal to the amount of energy transferred divided by the time it takes to transfer that energy. The units of power are watts (W) in the SI system, although other units such as horsepower and kilowatts are also commonly used.
How do we compute Energy?
The general formula for energy depends on the type of energy being considered, as different forms of energy have different mathematical representations. However, the most general and fundamental form of the formula for energy is based on the work-energy principle and is expressed as:

where E is the total energy of a system, W is the work done on the system, and U is the potential energy of the system.
Another formula for power systems is

where E is the total energy of a system, P is the power consumption in watts, and t is the duration of the measurement in hours.
The work-energy principle states that the work done on a system is equal to the change in its kinetic energy. This can be represented mathematically as:
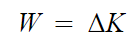
where W is the work done on the system and ΔK is the change in the system’s kinetic energy.
The potential energy of a system is a measure of the energy that is stored in the system due to its position or configuration. The potential energy can be calculated using various mathematical expressions, depending on the system and the type of potential energy involved. For example, the potential energy of an object in a gravitational field can be calculated using the formula:
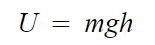
where U is the potential energy, m is the mass of the object, g is the acceleration due to gravity, and h is the height of the object above a reference point.
By combining the work-energy principle and the potential energy equation, we can obtain the general formula for energy:

where E is the total energy of the system, ΔK is the change in the system’s kinetic energy, and U is the potential energy of the system. This formula can be used to analyze and calculate the energy of various systems in physics and engineering.
How do we compute power?
Power is the rate at which work is done or energy is transferred, and it can be computed using the following formula:
Power = Work / Time
where Power is the amount of power in watts (W), Work is the amount of work done in joules (J), and Time is the amount of time taken in seconds (s).
Alternatively, if the energy expended is given instead of the work done, we can use the following formula:
Power = Energy / Time
where Energy is the amount of energy in joules (J), and Time is the amount of time taken in seconds (s).
In practice, power can also be computed by measuring other quantities related to work or energy transfer. For example, electrical power can be computed by measuring the voltage and current in a circuit using the following formula:
Power = Voltage x Current
where Power is the amount of power in watts (W), Voltage is the amount of voltage in volts (V), and Current is the amount of current in amperes (A).
Similarly, mechanical power can be computed by measuring the force and velocity of an object using the following formula:
Power = Force x Velocity
where Power is the amount of power in watts (W), Force is the amount of force in newtons (N), and Velocity is the amount of velocity in meters per second (m/s).
In general, the appropriate formula to use for computing power depends on the specific context and the type of energy transfer being considered.
Examples
Problem 1: A company wants to determine the energy consumption of a server that is running a workload for 2 hours. The server has a power consumption of 150 watts. What is the total energy consumption of the server in kilowatt-hours (kWh)?
Solution: To solve this problem, we can use the formula:
E= Pt
To convert watt-hours to kilowatt-hours, we can divide the watt-hours by 1,000.
Given that the server has a power consumption of 150 watts and is running a workload for 2 hours, we can calculate the total energy consumption as follows:
Energy = 150 watts x 2 hours = 300 watt-hours (Wh)
To convert watt-hours to kilowatt-hours, we can divide 300 Wh by 1,000:
Energy = 0.3 kilowatt-hours (kWh)
Therefore, the total energy consumption of the server is 0.3 kWh.
Problem 2: A data center has 100 servers that are running a workload for 8 hours per day, 5 days per week. Each server has a power consumption of 300 watts. The cost of electricity is 3 pesos per kilowatt-hour (kWh). What is the total energy consumption of the data center in kilowatt-hours per week? What is the weekly cost of electricity for the data center in pesos?
Solution: To solve this problem, we can use the formula:
Energy = Power x Time
where Energy is the energy consumption in watt-hours (Wh), Power is the power consumption in watts, and Time is the duration of the measurement in hours. To convert watt-hours to kilowatt-hours, we can divide the watt-hours by 1,000.
Given that there are 100 servers with a power consumption of 300 watts each, we can calculate the total power consumption of the data center as follows:
Total power consumption = 100 x 300 watts = 30,000 watts
Since the workload runs for 8 hours per day, 5 days per week, the total time is:
Total time = 8 hours/day x 5 days/week = 40 hours/week
Therefore, the total energy consumption of the data center per week is:
Energy = Total power consumption x Total time = 30,000 watts x 40 hours = 1,200,000 watt-hours (Wh)
To convert watt-hours to kilowatt-hours, we can divide 1,200,000 Wh by 1,000:
Energy = 1,200 kilowatt-hours (kWh)
Therefore, the total energy consumption of the data center per week is 1,200 kWh.
To calculate the weekly cost of electricity in pesos, we can multiply the total energy consumption by the cost of electricity per kWh:
Weekly cost = Energy x Cost of electricity = 1,200 kWh x 3 pesos/kWh = 3,600 pesos
Therefore, the weekly cost of electricity for the data center in pesos is 3,600 pesos.
Problem 3: A 1 kg object is lifted 5 meters from the ground. What is the total energy of the object when it is at this height? Assume that the acceleration due to gravity is 9.81 m/s^2.
Solution: In this problem, the object is lifted to a height of 5 meters, which means that its potential energy increases. The potential energy of an object is given by the formula:
U = mgh
where U is the potential energy, m is the mass of the object, g is the acceleration due to gravity, and h is the height of the object above a reference point.
In this case, the mass of the object is 1 kg, the acceleration due to gravity is 9.81 m/s^2, and the height is 5 meters. Therefore, the potential energy of the object is:
U = mgh = (1 kg) x (9.81 m/s^2) x (5 m) = 49.05 J
The work done on the object when it is lifted is equal to the change in its potential energy. This is given by the formula:
W = ΔU
where W is the work done and ΔU is the change in potential energy.
In this case, the object starts at ground level, where its potential energy is zero, and is lifted to a height of 5 meters, where its potential energy is 49.05 J. Therefore, the change in potential energy is:
ΔU = 49.05 J – 0 J = 49.05 J
The total energy of the object is given by the formula:
E = W + U
where E is the total energy.
In this case, the work done on the object is equal to the change in its potential energy, which is 49.05 J. Therefore, the total energy of the object is:
E = W + U = 49.05 J + 0 J = 49.05 J
Therefore, the total energy of the object when it is lifted to a height of 5 meters is 49.05 J.
Problem 3: A 7.80-g bullet moving at 575 m/s strikes the hand of a superhero, causing the hand to move 5.50 cm in the direction of the bullet’s velocity before stopping. (a) Use work and energy considerations to find the average force that stops the bullet. (b) Assuming the force is constant, determine how much time elapses between the moment the bullet.
Solution:
Given:


(b) Assuming the force is constant, we can use the formula for acceleration to determine how much time elapses between the moment the bullet strikes the hand and the moment it comes to rest. The acceleration of the bullet is equal to the force applied by the hand divided by the mass of the bullet, which is 7.80 g or 0.00780 kg.

Exercises:
- Problem: A 50-kg person climbs a flight of stairs that is 10 meters high. How much potential energy does the person gain?
- Problem: A roller coaster of mass 5000 kg is released from rest at the top of a hill 50 meters high. What is the total mechanical energy of the roller coaster at the bottom of the hill if there is no friction or air resistance?
- Problem: A car of mass 1500 kg is traveling on a straight road at 25 m/s when the driver applies the brakes. If the car comes to a stop in a distance of 50 meters, what is the average force applied by the brakes to stop the car?
Reviewer:
Change your quizlet setting to Multiple Choice only to avoid long typing. 🙂
References:
Jewett Jr, J. W., & Serway, R. A. (2021). Physics for scientists and engineers. Cengage Learning.


