Laboratory Activity: Exploring Differential Equations in RC Circuits Using Wolfram Alpha
Laboratory Activity: Exploring Differential Equations in RC Circuits Using Wolfram Alpha
Objective: Understand and solve differential equations for basic RC (Resistor-Capacitor) circuits using computational tools including Wolfram Alpha, MATLAB, and Python. Explore the theoretical foundations, numerical methods, and practical applications of RC circuit analysis.
Part 1: Theoretical Foundation of RC Circuits
1.1 Introduction to RC Circuit Theory
An RC circuit consists of a resistor (R) and a capacitor (C) connected in series or parallel. These fundamental circuits are ubiquitous in electronic systems, serving purposes such as filtering, timing, signal coupling, and power supply smoothing. Understanding RC circuits is essential for electrical engineering students as they demonstrate fundamental principles of energy storage, time-dependent behavior, and first-order system Dynamics.
The capacitor stores electrical energy in an electric field between its plates, while the resistor dissipates energy as heat. The interaction between these components creates time-dependent voltage and current behaviors that are described mathematically by first-order ordinary differential equations (ODEs).
1.2 Derivation of the RC Circuit Differential Equation
For a series RC circuit connected to a voltage source, we apply Kirchhoff’s Voltage Law (KVL) around the loop:
![]()
where ![]() is the source voltage,
is the source voltage, ![]() is the voltage across the resistor, and
is the voltage across the resistor, and ![]() is the voltage across the capacitor.
is the voltage across the capacitor.
Using Ohm’s Law for the resistor and the capacitor voltage-current relationship:
![]()
![]()
Substituting these relationships into the KVL equation:
![]()
Rearranging to standard first-order ODE form:
![]()
Or equivalently:
![]()
This is a first-order linear ordinary differential equation with constant coefficients, which has well-established analytical and numerical solution methods.
1.3 The Time Constant and Circuit Dynamics
The time constant ![]() (tau) is a fundamental parameter in RC circuit analysis, defined as:
(tau) is a fundamental parameter in RC circuit analysis, defined as:
![]()
The time constant represents the time required for the capacitor voltage to reach approximately 63.2% of its final value during charging, or to decay to approximately 36.8% of its initial value during discharging. This emerges naturally from the solution to the differential equation.
For a charging capacitor with initial voltage ![]() and source voltage
and source voltage ![]() , the analytical solution is:
, the analytical solution is:
![]()
When ![]() (uncharged capacitor):
(uncharged capacitor):
![]()
For a discharging capacitor (with ![]() ):
):
![]()
The time constant provides insight into circuit response speed and is crucial for designing timing circuits, filters, and signal processing applications.
Part 2: Laboratory Equipment and Setup
2.1 Required Equipment
| Equipment | Specifications | Quantity |
|---|---|---|
| DC Power Supply | 0-30V, 0-3A adjustable | 1 |
| Digital Multimeter (DMM) | 4½ digit, voltage and current measurement | 2 |
| Oscilloscope | 100 MHz, 2-channel minimum | 1 |
| Resistors | 1kΩ, 10kΩ, 100kΩ (±5%, ½W) | 3 each |
| Capacitors | 1μF, 10μF, 100μF (electrolytic, 25V) | 3 each |
| Breadboard | Standard solderless breadboard | 1 |
| Connecting Wires | 22 AWG, various lengths | 10+ |
| SPDT Switch | Toggle or push-button | 1 |
| Stopwatch | Digital, 0.01s resolution | 1 |
2.2 Safety Precautions
- Verify power supply voltage before connecting to circuit
- Observe correct polarity when connecting electrolytic capacitors
- Discharge capacitors completely before handling or modifying circuit
- Do not exceed component voltage and power ratings
- Ensure all connections are secure before applying power
- Use proper grounding techniques to prevent equipment damage
2.3 Circuit Assembly Procedure
- Measure and record actual component values using DMM (resistors and capacitors may vary from nominal values)
- Insert resistor and capacitor into breadboard in series configuration
- Connect SPDT switch to enable charging (position A: power supply connected) and discharging (position B: capacitor shorted through resistor)
- Connect oscilloscope probes across capacitor terminals
- Connect DMM in parallel with capacitor for voltage measurement
- Verify all connections before applying power
Part 3: Computational Analysis Using Wolfram Alpha
3.1 Getting Started with Wolfram Alpha
Wolfram Alpha is a powerful computational knowledge engine that can solve differential equations, generate plots, and perform symbolic mathematics. Access it at www.wolframalpha.com.
3.2 Exercise 1: Charging Capacitor Analysis
Circuit Parameters:
- Source voltage:
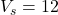 V
V - Resistance:
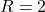 Ω
Ω - Capacitance:
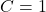 F
F - Initial condition:
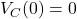 V
V
Step 1: Calculate the time constant:
![]()
Step 2: Input the differential equation into Wolfram Alpha:
solve dV/dt = (1/2)*(12 - V), V(0) = 0Step 3: Analyze the solution provided by Wolfram Alpha:
![]()
Step 4: Generate a plot by entering:
plot 12*(1 - e^(-t/2)) from t=0 to t=10Step 5: Calculate key time points:
- At
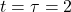 s:
s: 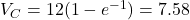 V (63.2% of
V (63.2% of 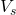 )
) - At
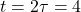 s:
s: 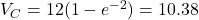 V (86.5% of
V (86.5% of 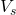 )
) - At
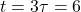 s:
s: 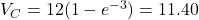 V (95.0% of
V (95.0% of 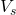 )
) - At
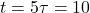 s:
s: 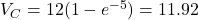 V (99.3% of
V (99.3% of 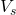 )
)
3.3 Exercise 2: Discharging Capacitor Analysis
Circuit Parameters:
- Resistance:
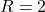 Ω
Ω - Capacitance:
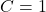 F
F - Initial condition:
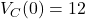 V (fully charged)
V (fully charged)
The differential equation for discharging:
![]()
Wolfram Alpha input:
solve dV/dt = -V/2, V(0) = 12Solution:
![]()
Plot command:
plot 12*e^(-t/2) from t=0 to t=103.4 Comparative Analysis
To visualize both charging and discharging on the same plot:
plot {12*(1-e^(-t/2)), 12*e^(-t/2)} from t=0 to t=10Key Observations:
- Both curves are exponential but mirror each other
- Charging curve approaches
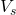 asymptotically from below
asymptotically from below - Discharging curve approaches zero asymptotically from above
- Both have the same time constant
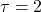 s
s - Rate of change is maximum at
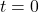 for both processes
for both processes - After 5τ (10s), both processes are essentially complete (>99%)
Part 4: MATLAB and Python Implementation
4.1 MATLAB Code for RC Circuit Analysis
% RC Circuit Analysis - Charging and Discharging
% Parameters
R = 2; % Resistance in Ohms
C = 1; % Capacitance in Farads
Vs = 12; % Source voltage in Volts
tau = R * C; % Time constant
% Time vector
t = 0:0.01:10; % 0 to 10 seconds
% Analytical solutions
Vc_charging = Vs * (1 - exp(-t/tau));
Vc_discharging = Vs * exp(-t/tau);
% Current during charging and discharging
Ic_charging = (Vs/R) * exp(-t/tau);
Ic_discharging = -(Vs/R) * exp(-t/tau);
% Create figure with subplots
figure('Position', [100, 100, 1200, 800]);
% Plot 1: Voltage comparison
subplot(2,2,1);
plot(t, Vc_charging, 'b-', 'LineWidth', 2);
hold on;
plot(t, Vc_discharging, 'r-', 'LineWidth', 2);
plot([tau tau], [0 Vs], 'k--', 'LineWidth', 1);
xlabel('Time (s)', 'FontSize', 12);
ylabel('Voltage (V)', 'FontSize', 12);
title('RC Circuit: Voltage vs Time', 'FontSize', 14);
legend('Charging', 'Discharging', '\tau = RC', 'Location', 'best');
grid on;
% Plot 2: Current comparison
subplot(2,2,2);
plot(t, Ic_charging*1000, 'b-', 'LineWidth', 2);
hold on;
plot(t, Ic_discharging*1000, 'r-', 'LineWidth', 2);
xlabel('Time (s)', 'FontSize', 12);
ylabel('Current (mA)', 'FontSize', 12);
title('RC Circuit: Current vs Time', 'FontSize', 14);
legend('Charging', 'Discharging', 'Location', 'best');
grid on;
% Plot 3: Phase plane (V vs I)
subplot(2,2,3);
plot(Vc_charging, Ic_charging*1000, 'b-', 'LineWidth', 2);
hold on;
plot(Vc_discharging, abs(Ic_discharging)*1000, 'r-', 'LineWidth', 2);
xlabel('Voltage (V)', 'FontSize', 12);
ylabel('Current (mA)', 'FontSize', 12);
title('Phase Plane: Current vs Voltage', 'FontSize', 14);
legend('Charging', 'Discharging', 'Location', 'best');
grid on;
% Plot 4: Energy stored in capacitor
E_charging = 0.5 * C * Vc_charging.^2;
E_discharging = 0.5 * C * Vc_discharging.^2;
subplot(2,2,4);
plot(t, E_charging, 'b-', 'LineWidth', 2);
hold on;
plot(t, E_discharging, 'r-', 'LineWidth', 2);
xlabel('Time (s)', 'FontSize', 12);
ylabel('Energy (J)', 'FontSize', 12);
title('Energy Stored in Capacitor', 'FontSize', 14);
legend('Charging', 'Discharging', 'Location', 'best');
grid on;
% Display key values
fprintf('Time Constant (tau): %.2f seconds\n', tau);
fprintf('Voltage at t=tau (charging): %.2f V (%.1f%% of Vs)\n', ...
Vs*(1-exp(-1)), 100*(1-exp(-1)));
fprintf('Voltage at t=tau (discharging): %.2f V (%.1f%% of Vs)\n', ...
Vs*exp(-1), 100*exp(-1));
fprintf('Time to reach 95%% of Vs: %.2f seconds (%.2f * tau)\n', ...
-tau*log(0.05), -log(0.05));
fprintf('Time to reach 99%% of Vs: %.2f seconds (%.2f * tau)\n', ...
-tau*log(0.01), -log(0.01));
% Numerical solution using ODE45
[t_ode, V_ode] = ode45(@(t,V) (Vs-V)/(R*C), [0 10], 0);
fprintf('\nNumerical vs Analytical Solution Error (RMS): %.2e V\n', ...
sqrt(mean((interp1(t_ode, V_ode, t) - Vc_charging).^2)));
4.2 Python Code for RC Circuit Analysis
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
from scipy.optimize import curve_fit
# RC Circuit Analysis - Charging and Discharging
# Parameters
R = 2.0 # Resistance in Ohms
C = 1.0 # Capacitance in Farads
Vs = 12.0 # Source voltage in Volts
tau = R * C # Time constant
# Time vector
t = np.linspace(0, 10, 1000)
# Analytical solutions
Vc_charging = Vs * (1 - np.exp(-t/tau))
Vc_discharging = Vs * np.exp(-t/tau)
# Current during charging and discharging
Ic_charging = (Vs/R) * np.exp(-t/tau)
Ic_discharging = -(Vs/R) * np.exp(-t/tau)
# Numerical solution using ODE solver
def rc_charging(V, t):
return (Vs - V) / (R * C)
def rc_discharging(V, t):
return -V / (R * C)
V_charging_numerical = odeint(rc_charging, 0, t)
V_discharging_numerical = odeint(rc_discharging, Vs, t)
# Create comprehensive plots
fig, axes = plt.subplots(2, 2, figsize=(15, 10))
# Plot 1: Voltage comparison
axes[0, 0].plot(t, Vc_charging, 'b-', linewidth=2, label='Charging (Analytical)')
axes[0, 0].plot(t, Vc_discharging, 'r-', linewidth=2, label='Discharging (Analytical)')
axes[0, 0].plot(t, V_charging_numerical, 'b--', linewidth=1, label='Charging (Numerical)')
axes[0, 0].plot(t, V_discharging_numerical, 'r--', linewidth=1, label='Discharging (Numerical)')
axes[0, 0].axvline(x=tau, color='k', linestyle='--', linewidth=1, label=f'τ = {tau}s')
axes[0, 0].axhline(y=Vs*0.632, color='gray', linestyle=':', linewidth=1)
axes[0, 0].set_xlabel('Time (s)', fontsize=12)
axes[0, 0].set_ylabel('Voltage (V)', fontsize=12)
axes[0, 0].set_title('RC Circuit: Voltage vs Time', fontsize=14, fontweight='bold')
axes[0, 0].legend(loc='best')
axes[0, 0].grid(True, alpha=0.3)
# Plot 2: Current comparison
axes[0, 1].plot(t, Ic_charging*1000, 'b-', linewidth=2, label='Charging')
axes[0, 1].plot(t, Ic_discharging*1000, 'r-', linewidth=2, label='Discharging')
axes[0, 1].set_xlabel('Time (s)', fontsize=12)
axes[0, 1].set_ylabel('Current (mA)', fontsize=12)
axes[0, 1].set_title('RC Circuit: Current vs Time', fontsize=14, fontweight='bold')
axes[0, 1].legend(loc='best')
axes[0, 1].grid(True, alpha=0.3)
# Plot 3: Power dissipation in resistor
P_charging = Ic_charging**2 * R
P_discharging = Ic_discharging**2 * R
axes[1, 0].plot(t, P_charging, 'b-', linewidth=2, label='Charging')
axes[1, 0].plot(t, P_discharging, 'r-', linewidth=2, label='Discharging')
axes[1, 0].set_xlabel('Time (s)', fontsize=12)
axes[1, 0].set_ylabel('Power (W)', fontsize=12)
axes[1, 0].set_title('Power Dissipation in Resistor', fontsize=14, fontweight='bold')
axes[1, 0].legend(loc='best')
axes[1, 0].grid(True, alpha=0.3)
# Plot 4: Energy stored in capacitor
E_charging = 0.5 * C * Vc_charging**2
E_discharging = 0.5 * C * Vc_discharging**2
axes[1, 1].plot(t, E_charging, 'b-', linewidth=2, label='Charging')
axes[1, 1].plot(t, E_discharging, 'r-', linewidth=2, label='Discharging')
axes[1, 1].set_xlabel('Time (s)', fontsize=12)
axes[1, 1].set_ylabel('Energy (J)', fontsize=12)
axes[1, 1].set_title('Energy Stored in Capacitor', fontsize=14, fontweight='bold')
axes[1, 1].legend(loc='best')
axes[1, 1].grid(True, alpha=0.3)
plt.tight_layout()
plt.savefig('rc_circuit_analysis.png', dpi=300, bbox_inches='tight')
plt.show()
# Print key calculations
print(f"Time Constant (τ): {tau:.2f} seconds")
print(f"Voltage at t=τ (charging): {Vs*(1-np.exp(-1)):.2f} V ({100*(1-np.exp(-1)):.1f}% of Vs)")
print(f"Voltage at t=τ (discharging): {Vs*np.exp(-1):.2f} V ({100*np.exp(-1):.1f}% of Vs)")
print(f"Time to reach 95% of Vs: {-tau*np.log(0.05):.2f} seconds ({-np.log(0.05):.2f} × τ)")
print(f"Time to reach 99% of Vs: {-tau*np.log(0.01):.2f} seconds ({-np.log(0.01):.2f} × τ)")
# Error analysis
error_charging = np.sqrt(np.mean((V_charging_numerical.flatten() - Vc_charging)**2))
error_discharging = np.sqrt(np.mean((V_discharging_numerical.flatten() - Vc_discharging)**2))
print(f"\nNumerical vs Analytical Solution Error (RMS):")
print(f" Charging: {error_charging:.2e} V")
print(f" Discharging: {error_discharging:.2e} V")
# Total energy dissipated
E_dissipated_charging = np.trapz(P_charging, t)
E_dissipated_discharging = np.trapz(P_discharging, t)
print(f"\nTotal Energy Dissipated in Resistor:")
print(f" Charging: {E_dissipated_charging:.2f} J")
print(f" Discharging: {E_dissipated_discharging:.2f} J")
Part 5: LTSpice Circuit Simulation
5.1 LTSpice Setup and Simulation
LTSpice is a powerful SPICE-based analog circuit simulator. To simulate the RC circuit:
Circuit Netlist for Charging:
* RC Circuit Charging Analysis
V1 N001 0 PULSE(0 12 0 1n 1n 10 20)
R1 N001 N002 2
C1 N002 0 1 IC=0
.tran 0 10 0 0.01
.backanno
.end
Circuit Netlist for Discharging:
* RC Circuit Discharging Analysis
V1 N001 0 PULSE(12 0 0 1n 1n 10 20)
R1 N001 N002 2
C1 N002 0 1 IC=12
.tran 0 10 0 0.01
.backanno
.end
5.2 Simulation Directives
- .tran: Transient analysis from 0 to 10 seconds
- PULSE: Voltage source that switches between levels
- IC: Initial condition for capacitor voltage
- Add voltage and current probes to visualize waveforms
- Use .meas commands to automatically extract rise/fall times
Measurement Commands:
.meas TRAN Vtau FIND V(N002) AT {2}
.meas TRAN T63 WHEN V(N002)=7.58
.meas TRAN T95 WHEN V(N002)=11.4
Part 6: Experimental Scenarios and Analysis
Scenario 1: Effect of Varying Resistance
Objective: Investigate how resistance affects charging/discharging time.
Procedure:
- Fix capacitance at C = 10μF
- Test with R = 1kΩ, 10kΩ, 100kΩ
- Measure time to reach 63.2% of Vs for each resistor
- Record voltage vs. time data
Expected Results:
| R (kΩ) | C (μF) | τ (ms) | Time to 63.2% Vs |
|---|---|---|---|
| 1 | 10 | 10 | ~10 ms |
| 10 | 10 | 100 | ~100 ms |
| 100 | 10 | 1000 | ~1 s |
Scenario 2: Effect of Varying Capacitance
Objective: Analyze capacitance impact on circuit dynamics.
Procedure:
- Fix resistance at R = 10kΩ
- Test with C = 1μF, 10μF, 100μF
- Measure time constant for each configuration
- Compare theoretical vs. experimental values
Scenario 3: Temperature Effects on Components
Objective: Study temperature coefficient effects on RC behavior.
Procedure:
- Measure component values at room temperature (25°C)
- Heat components to 50°C (using heat gun or oven)
- Remeasure component values and time constant
- Calculate temperature coefficient from measurements
Theory: Electrolytic capacitors typically have negative temperature coefficients (-2% to -5% per °C), while resistors vary based on composition.
Scenario 4: Non-Ideal Capacitor Behavior (ESR)
Objective: Investigate effects of equivalent series resistance (ESR).
Modified Circuit Model: Real capacitors have internal resistance (ESR) that affects performance, especially at high frequencies.
Procedure:
- Measure ESR of electrolytic capacitor using LCR meter
- Include ESR in simulation model
- Compare ideal vs. non-ideal capacitor response
- Calculate power dissipation in ESR
Scenario 5: Multiple Time Constant Circuits
Objective: Analyze cascaded RC networks with different time constants.
Circuit: Two RC stages in series (R1-C1 followed by R2-C2)
Procedure:
- Design circuit with τ1 = 10ms and τ2 = 100ms
- Apply step input and measure voltage at both capacitors
- Compare single vs. dual time constant response
- Analyze frequency response using Bode plots
Scenario 6: RC Circuit as Low-Pass Filter
Objective: Demonstrate RC circuit filtering properties.
Cutoff Frequency:
![]()
Procedure:
- Calculate theoretical cutoff frequency
- Apply sinusoidal input at various frequencies (0.1fc to 10fc)
- Measure output amplitude and phase shift
- Plot frequency response (magnitude and phase)
- Verify -3dB point at cutoff frequency
- Confirm -20dB/decade roll-off in stopband
Part 7: Error Analysis and Uncertainty
7.1 Sources of Experimental Error
- Component Tolerances:
- Resistors: Typically ±5% (color code: gold band)
- Capacitors: ±10% to ±20% (especially electrolytic types)
- Impact: Time constant can vary by ±15% to ±25%
- Measurement Instrument Errors:
- DMM accuracy: ±(0.5% of reading + 2 digits)
- Oscilloscope timebase: ±0.01%
- Probe loading effects on high-impedance circuits
- Environmental Factors:
- Temperature variations affecting component values
- Humidity effects on capacitor performance
- Power supply noise and ripple
- Parasitic Effects:
- Stray capacitance in breadboard (~2-5pF per connection)
- Lead inductance (~1nH/mm)
- Contact resistance in breadboard connections
7.2 Uncertainty Calculations
Time Constant Uncertainty:
Using propagation of uncertainty for τ = RC:
![Rendered by QuickLaTeX.com \[\frac{\delta\tau}{\tau} = \sqrt{\left(\frac{\delta R}{R}\right)^2 + \left(\frac{\delta C}{C}\right)^2}\]](https://hamnus.com/wp-content/ql-cache/quicklatex.com-93293a56510dd75b76cd515ee5edc821_l3.png)
Example: For R = 10kΩ ±5% and C = 10μF ±10%:
![]()
![]()
7.3 Minimizing Experimental Errors
- Use precision resistors (±1% or better) when accuracy is critical
- Measure actual component values before circuit assembly
- Allow components to stabilize at ambient temperature
- Use short leads to minimize parasitic effects
- Account for oscilloscope probe input capacitance (~15pF)
- Repeat measurements multiple times and average results
- Compare experimental results with simulation to identify systematic errors
Part 8: Report Writing and Documentation
8.1 Laboratory Report Structure
Your comprehensive report should include the following sections:
- Title Page: Include lab title, your name, date, course information
- Abstract: 150-200 word summary of objectives, methods, and key findings
- Introduction: Background on RC circuits, theoretical foundation, objectives
- Theory: Derivation of differential equations, analytical solutions, key equations
- Experimental Setup: Equipment list, circuit diagrams, measurement procedures
- Results: Data tables, graphs, computational outputs, simulation screenshots
- Analysis: Comparison of theoretical, computational, and experimental results
- Error Analysis: Sources of error, uncertainty calculations, improvement suggestions
- Discussion: Interpretation of results, practical applications, limitations
- Conclusion: Summary of findings, learning outcomes, future work
- References: IEEE format citations
- Appendices: Raw data, code listings, additional plots
8.2 Data Presentation Guidelines
- Use consistent units throughout (SI preferred)
- Include error bars on experimental data points
- Label all axes with quantities and units
- Use descriptive captions for figures and tables
- Number equations, figures, and tables sequentially
- Reference all figures and tables in text
8.3 Sample Data Table
| Time (s) | Vc Theoretical (V) | Vc Experimental (V) | Error (%) |
|---|---|---|---|
| 0.00 | 0.00 | 0.02 | – |
| 0.05 | 3.58 | 3.52 | 1.68 |
| 0.10 | 5.65 | 5.59 | 1.06 |
| 0.20 | 7.97 | 7.88 | 1.13 |
| 0.50 | 10.78 | 10.65 | 1.21 |
| 1.00 | 11.75 | 11.68 | 0.60 |
Part 9: Learning Outcomes and Assessment
9.1 Expected Learning Outcomes
Upon completion of this laboratory activity, students should be able to:
- Derive and solve first-order differential equations for RC circuits
- Calculate and interpret the time constant τ = RC
- Use computational tools (Wolfram Alpha, MATLAB, Python) for circuit analysis
- Design and build RC circuits for specific time constant requirements
- Perform accurate experimental measurements using oscilloscope and DMM
- Simulate circuits using SPICE-based software (LTSpice)
- Analyze sources of error and calculate experimental uncertainty
- Compare theoretical, computational, and experimental results
- Document findings in professional technical report format
- Apply RC circuit principles to practical applications (filters, timers, coupling)
9.2 Assessment Rubric
| Category | Weight | Criteria |
|---|---|---|
| Theoretical Understanding | 20% | Correct derivation of ODEs, understanding of time constant, analytical solutions |
| Computational Analysis | 20% | Proper use of Wolfram Alpha, MATLAB/Python code functionality, simulation accuracy |
| Experimental Work | 20% | Circuit assembly, measurement technique, data collection quality |
| Data Analysis | 15% | Comparison of results, error analysis, uncertainty calculations |
| Report Quality | 15% | Organization, clarity, graphs/tables, professional presentation |
| Discussion & Conclusions | 10% | Insight, critical thinking, practical applications, limitations |
References
[1] A. V. Oppenheim, A. S. Willsky, and S. H. Nawab, Signals and Systems, 2nd ed. Upper Saddle River, NJ: Prentice Hall, 1997.
[2] C. K. Alexander and M. N. O. Sadiku, Fundamentals of Electric Circuits, 6th ed. New York, NY: McGraw-Hill, 2017.
[3] R. C. Dorf and J. A. Svoboda, Introduction to Electric Circuits, 9th ed. Hoboken, NJ: Wiley, 2014.
[4] P. Horowitz and W. Hill, The Art of Electronics, 3rd ed. New York, NY: Cambridge University Press, 2015.
[5] J. W. Nilsson and S. A. Riedel, Electric Circuits, 11th ed. Upper Saddle River, NJ: Pearson, 2019.
[6] IEEE Standard for Transitions, Pulses, and Related Waveforms, IEEE Std 181-2011, IEEE, New York, NY, 2011.
[7] R. L. Burden and J. D. Faires, Numerical Analysis, 9th ed. Boston, MA: Brooks/Cole, 2011.
[8] S. Wolfram, The Mathematica Book, 5th ed. Champaign, IL: Wolfram Media, 2003.
[9] MATLAB Documentation, MathWorks, [Online]. Available: https://www.mathworks.com/help/matlab/
[10] LTspice XVII User Guide, Analog Devices, 2021. [Online]. Available: https://www.analog.com/en/design-center/design-tools-and-calculators/ltspice-simulator.html
Appendix A: Quick Reference Formulas
Time Constant: ![]()
Charging (V₀ = 0): ![]()
Discharging: ![]()
Current (charging): ![]()
Energy in capacitor: ![]()
Power in resistor: ![]()
Cutoff frequency: ![]()
Time to reach X%: ![]()
Appendix B: Troubleshooting Guide
| Problem | Possible Cause | Solution |
|---|---|---|
| Capacitor not charging | Reversed polarity (electrolytic) | Check polarity markings, reconnect correctly |
| Time constant too different from calculated | Component values outside tolerance | Measure actual R and C values, recalculate τ |
| Oscilloscope shows no waveform | Incorrect trigger settings | Set trigger to edge mode, adjust trigger level |
| Voltage exceeds supply voltage | Capacitor initially charged | Discharge capacitor completely before starting |
| Erratic measurements | Poor breadboard connections | Ensure all connections are firm and secure |
Explore Related Engineering Topics
- Introduction to Differential Equations – Master the mathematical foundations
- Wolfram Alpha for Differential Equations – Complete guide to computational solving
- Numerical Methods in Engineering – Alternative solution techniques
- Computer Engineering Career Guide – See where these skills lead

