The Newton-Raphson method is an iterative numerical method used to find the root of a function. It is named after Sir Isaac Newton and Joseph Raphson, who independently developed the method in the 17th century.
The Newton-Raphson method starts with an initial guess for the root of a function and then uses the derivative of the function to find a better approximation of the root. This process is repeated until the desired level of accuracy is achieved.
The general formula for the Newton-Raphson method is:
x_{n+1} = x_n – f(x_n)/f'(x_n)
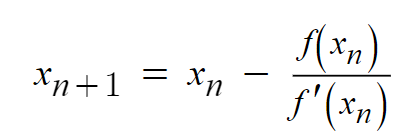
where x_n is the current approximation of the root, f(x_n) is the value of the function at x_n, and f'(x_n) is the derivative of the function at x_n. The next approximation of the root, x_{n+1}, is then calculated using this formula.
To use the Newton-Raphson method, we need to have an initial guess for the root and an expression for the derivative of the function. The method can converge quickly to the root if the initial guess is close to the actual root and the function is well-behaved (i.e., has a continuous derivative).
However, the method may fail to converge or converge to a different root if the initial guess is too far from the actual root or if the function has multiple roots or discontinuities.
The Newton-Raphson method is widely used in various fields of engineering, physics, and mathematics to solve equations and find roots of complex functions.
What is the advantage of Newton-Raphson method?
The Newton-Raphson method is an iterative algorithm used for finding the roots of a real-valued function. Here are some advantages of the Newton-Raphson method:
- Convergence: The Newton-Raphson method is known for its fast convergence. This means that it requires fewer iterations to converge to the root of a function compared to other iterative methods.
- High accuracy: The method is known to be highly accurate, especially when the initial guess is close to the actual root. The accuracy can be improved by using a better initial guess.
- General applicability: The Newton-Raphson method can be used to find the roots of many different types of functions, including polynomials, trigonometric functions, and exponential functions.
- Easy to implement: The method is relatively easy to implement and can be used with a computer program to automate the calculations.
- Efficiency: The Newton-Raphson method can be used to solve complex problems in a short amount of time, making it a popular choice in many scientific and engineering applications.
The Secant Method
The secant method is an iterative algorithm used to find an approximation of the root of a function. It is a modification of the Newton-Raphson method that uses two initial guesses instead of one. The algorithm starts by selecting two initial guesses, x0 and x1, that bracket the root of the function. The method then computes the value of the function at these two points, f(x0) and f(x1), and uses them to compute the slope between the two points. The next approximation of the root is then calculated using the formula:
x2 = x1 – f(x1) * (x1 – x0) / (f(x1) – f(x0))
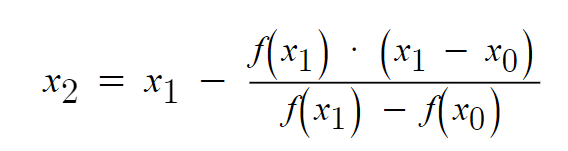
This formula computes a new guess for the root based on the slope between the two previous guesses. The algorithm then checks the error between the previous and current approximations. If the error is below a predetermined tolerance level, the algorithm stops and outputs the current approximation as the root. If not, the algorithm uses the current guess as the new x1 and the previous guess as the new x0, and repeats the process until the desired level of accuracy is achieved.
The secant method is a powerful tool for finding roots of functions because it is relatively simple to implement and does not require the calculation of derivatives. However, it may converge more slowly than the Newton-Raphson method and may require more iterations to achieve the same level of accuracy. The method is especially useful when the derivative is difficult to compute or when the function is computationally expensive.
Advantages of the Secant Method
The secant method is a root-finding algorithm that offers several advantages over other iterative methods:
- No need for derivatives: The secant method does not require the calculation of derivatives, making it a useful tool when derivatives are not available or difficult to compute.
- Simplicity: The secant method is relatively simple to implement, requiring only two initial guesses to get started.
- Applicability: The secant method can be used to find the roots of many different types of functions, including nonlinear equations, transcendental equations, and differential equations.
- Robustness: The secant method is robust in the sense that it can handle many different types of functions, and it is not affected by the presence of multiple roots or discontinuities.
- Efficiency: The secant method can be an efficient method for finding roots, especially when the function is computationally expensive or the derivative is difficult to compute.
The Difference between the Newton-Raphson method and the Secant Method.
Both the Newton-Raphson method and the secant method are iterative algorithms used for finding the roots of a real-valued function. However, there are some differences between the two methods:
- Initial Guesses: The Newton-Raphson method uses a single initial guess, while the secant method uses two initial guesses.
- Derivative: The Newton-Raphson method requires the computation of the derivative of the function, while the secant method does not require the computation of the derivative.
- Convergence Rate: The Newton-Raphson method converges faster than the secant method in most cases, which means that it requires fewer iterations to reach a solution.
- Accuracy: The Newton-Raphson method is more accurate than the secant method when the initial guess is close to the actual root, while the secant method can be more accurate when the initial guess is far from the actual root.
- Robustness: The secant method is more robust than the Newton-Raphson method when it comes to handling functions that have multiple roots or discontinuities.
- Efficiency: The secant method may be more efficient than the Newton-Raphson method when the function is computationally expensive, as it requires fewer function evaluations per iteration.